|
Problem description and solving approach The Steiner tree problem in graphs (SPG) can be described as follows: Given an undirected connected graph
and a set 
The solving approach of SCIP-Jack can be dissected into three major components: First, problem specific preprocessing is extremely important. Apart from some pathological instances specifically constructed to defy presolving techniques, preprocessing is often able to significantly reduce instances or even solve them. Second, heuristics are needed, especially for hard instances, to find good or even optimal solutions. Finally, the core of our approach is constituted by a branch-and-cut procedure used to compute lower bounds and prove optimality. The problem can be formulated using the directed equivalent of the SPG, the Steiner arborescence problem (SAP): Given a directed graph
where Since the model potentially contains an exponential number of constraints, a separation approach is employed. Violated constraints are separated during the execution of the branch-and-cut algorithm. In addition to Steiner problems in graphs there exist several variations. The following Steiner problem variants can be solved by SCIP-JACK, by transforming them to a Steiner arborescence problem, and in some cases introducing additional constraints: -Steiner arborescence problems, -rectilinear Steiner minimum tree problems, -node-weighted Steiner tree problems, -prize-collecting Steiner tree problems, -rooted prize-collecting Steiner tree problems, -maximum-weight connected subgraph problems, -degree-constrained Steiner tree problems, -group Steiner tree problems, and -hop-honstrained directed Steiner tree problems. A far more intricate description of SCIP-Jack and its various components can be found in "A generic approach to solving the Steiner tree problem and variants" by D. Rehfeldt. |

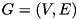 , costs
, costs ![\[ c: E \rightarrow \mathcal{Q}^+ \]](form_1.png)
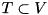 of terminals, the problem is to find a minimum-weight tree
of terminals, the problem is to find a minimum-weight tree  that spans
that spans 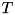 . Each tree
. Each tree 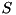 that spans
that spans 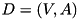 , a root
, a root 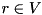 , costs
, costs 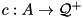 and a set
and a set  such that for all
such that for all 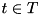 ,
, 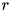 to
to 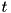 is called Steiner arborescence. Thereupon, a Steiner arborescence
is called Steiner arborescence. Thereupon, a Steiner arborescence 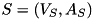 is required that minimizes
is required that minimizes 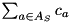 . An SPG can be transformed to an SAP by replacing each edge with two anti-parallel arcs of the same cost and distinguishing an arbitrary terminal as the root. This transformation results in a one-to-one correspondence between the respective solution sets. Introducing variables
. An SPG can be transformed to an SAP by replacing each edge with two anti-parallel arcs of the same cost and distinguishing an arbitrary terminal as the root. This transformation results in a one-to-one correspondence between the respective solution sets. Introducing variables 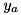 for
for 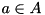 with the interpretation that
with the interpretation that 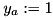 if and only if
if and only if 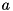 is in the Steiner arborecence, and
is in the Steiner arborecence, and 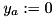 otherwise, we obtain the integer program:
otherwise, we obtain the integer program:![\[ \begin{array}[t]{rll} \min {c}^T y\\ \\ y(\delta^+(W))&\geq& 1, ~~~ \forall , W\subset V, r\in W, (V\setminus W)\cap T\neq \emptyset\\ y(\delta^-(v))& \left\{{\begin{array}{l} = \\ = \\ \leq \end{array}}\right. & {\begin{array}{l} 0, \mbox{if } v=r;\\ 1, \mbox{if } v\in T\setminus{r};\\ 1, \mbox{if } v\in N; \end{array}} \hspace{2.9mm}\forall v \in V \\ y(\delta^-(v))&\leq& y(\delta^+(v)), \hspace{10.5mm}\forall v\in N;\\ y(\delta^-(v))&\geq& y_a, \hspace{20.2mm}\forall a\in\delta^+(v), v\in N;\\ 0\leq y_a&\leq& 1, \hspace{22mm}\forall a\in A;\\ y_a&\in& \{0,1\}, \hspace{15.1mm}\forall a\in A, \end{array} \]](form_20.png)
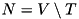 ,
, 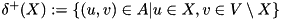 ,
, 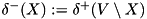 for
for 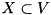 i.e.,
i.e., 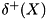 is the set of all arcs going out of and
is the set of all arcs going out of and 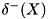 the set of all arcs going into
the set of all arcs going into 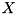 .
.